統計学などで「95%の確率で正しい」などという言葉をよく聞くと思う。
この95%の精度を体感いただこう。以下の文章を読んでほしい。
宮沢賢治の「銀河鉄道の夜」の冒頭である。
「ではみなさんは、そういうふうに川だと云れたり、乳の流れたあとだと云われたりしていたこのぼんやりと白いものがほんとうは何かご承知ですか。」先生は、黒板に吊るした大きな黒い星座の図の、上から下へ白くけぶった銀河帯のようなところを指さしながら、みんなに問いをかけました。
以下はどうでしょうか?
「ではみなさんに、そういうふうに川だと云れたけ、乳の流れたあとだと云われたりしていけこのぼんやりと白いあのがほんとうは何かご承知ですか。」先生は、黒板に吊るこた大きな黒い星座の図の、上なら下へ白くけぶった銀河帯のよほなところを指さしながら、みんなに問いをかけました。
139文字の5%とは6.95なので、7文字の間違いをいれてみた。
おそらくこんな本があったら、みんな怒り出すのではないだろうか?
95%の信頼性ってこんなもんなんです。
にもかかわらず、私達は95%と聞くと、絶対だ、100%に近いと考えます。
では60%くらいの信頼性と聞くと、どう感じますか?
ほとんどの人が「あやしいな」と感じるのではないでしょうか?
つまり
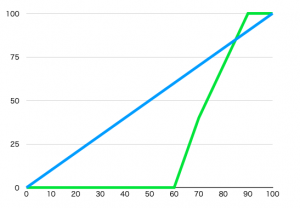
水平方向が理論値で、縦方向が人の感覚的な確率です。
青色は理論どおりの直線です。緑色が今議論している人が感じる確率です。
数字的にはいろいろなご意見があるでしょうけれども、私達は0か100で物事を考えがちで、あいまいな部分をできるだけ避けたいと考えていないでしょうか?
一方、確率のように見えて、そうじゃない世界があります。
しばしばスーパーコンピューター(スパコン)の計算結果が発表されていますよね。
くしゃみの飛沫感染などがあります。
このような計算結果で、単なる数値ではなく濃淡で示されると私達は納得します。
考えてみれば伝統的な統計学は、このような計算がたいへんだから計算量を省略するために考え出された技法といっていいと思います。
今ならデータを全部、プロットして母集団を観察できることも多いです。
昔はそれが大変だったから、数学的な理想的母集団を作って計算して推定したわけです。
プラスマイナス5%を例外とするなんてフィッシャー大先生が根拠なく決めたことだといいます。
たんなる95%の可能性から出てきた結果をいじっていても判断を誤ります。
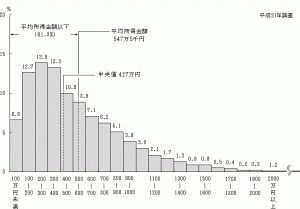
何度か示していますが、日本の所得分布もそうですね。
このグラフで平均になんの意味があるのでしょうか?
分布を見れば「日本国民の多くは所得が200万円から300万円であり、平均とされる400万円所得がある人は高所得なほうだ」となりませんか?
伝統的統計学の推定を議論する時には、このように母集団(全体)の分布を必ずみてください。
ね、伝統的な統計学はイマドキのコンピューティングパワーの前では最強でもなんでもないです。