常々、日本人は確率を扱うことが下手だと書き続けてきた。
ちょい暇なので説明を試みてみる。
これ知ったら、相当に人生で得をするはずだ。
伝統的な確率の話から始める。
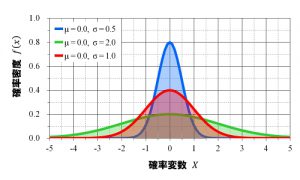
もっとも重要な概念は正規分布であることは異論がないだろう。
この図をよく見て考えていただきたい。
考えるポイントは
- 確率とは無限回の試行を前提とした抽象的な概念である
- 平均と分散によって図のようにきまるが、分散が大きいと山は低くなり平均以外がとても多い
- 一回だけの試行を取り上げると、果たしてそれが分布のどこにあたるのかわからないことが多々ある。
言い換えると、平均も分散もわからない場合、正規分布かどうかすらわからない。 - 95%の確率でという言葉に素人は踊りすぎ。5%の例外があるのだ。
5%とは文章で20文字ならんでいて1文字誤字があることに等しい。
そんな読みづらい文章をあなたは絶対のものとして受け入れられるだろうか?
ここからいろんなことがわかる。
例えば、株を買う場合に「ボリンジャーバンド」というものがある。値動きが正規分布に従うとして分散から外れたところを拾うのだが、株価の値動きは正規分布ではないことがすでにわかっている。
にもかかわらず、ボリンジャーバンドの信奉者はいまだに多い。
例えば、いい大学に行ったらよい仕事につけるから、よい人生になる、と考える人は世間知らずに多い。
よい仕事が実入りのいい仕事ではなく、実は他人に威張れる有名企業であるという基準が本音であるにもかかわらず、上のような概念を漠然と信じている。それも根拠はすべて伝聞であって自分ではなにひとつ調べていないにもかかわらず人生観にまでなっている。
そして人生は一度、もしくは有限回の試行であり、確率を単純には応用できない。
少なくとも確率から学ぶべきことは、
例えば、一度失敗してもしつこくトライすると成功確率は飛躍的にあがる。1/10の成功確率であることを2回やれば1/5, 三回やれば1/3、4回やれば2/5、5回やると実に1/2となる。
線形でないことに着目してほしい。
正規分布には疑念がつきまとうがここでは、人生への活かし方が重要なので割愛。
もうひとつ、よくわからない性質。
確率には「大数の法則」があり、たくさん試行すればそれに従うという。
しかし、人でも自然でもいいけれど、あまり起こりそうにないシチュエーション(事象)においても法則が働くと主張することはとても不思議だ。
たとえば、人の死亡率というものを求めるとする。
最終的には100%だが、通常はデータを集め統計をとる。
それは因果関係にはまったく言及しないで単に集めたデータだ。
しかし、病気の治療が発達し、どれくらい羅患した人を救えるかと計算を始め様子を見ているとその数値に従う。
まるで誰かが計算したから確率が決まったかのような気持ちになってしまう。
たとえば、コインのオモテウラが出る確率が1/2とする。
一度目 オモテ、二度目 オモテ、三度目 オモテ、だったら四度目くらいにウラが出るだろうと我々は考えるが、数学的にはやはり1/2だという。
しかし、オモテーオモテーオモテーウラが出る確率は実に1/16となる。
大数の法則はたしかに「いつから計算値に回復するか」はなにもいわない。
何度も同じ試行を繰り返していたら「いつしか」だという。
そのコインを利用して、100人の人に丁半賭博をさせる。
結果は勝っている人と負けている人が50人、50人に近づき、全員が引き分けになるわけじゃないことが知られている。
確率をいじっている時に感覚的に納得できないことは多い。
だからギャンブラーは「2度あることは3度ある」にかけるのだ。
ところが結果を見たら確率が変わる、という感覚的にもとてもフィットする考え方がある。
多くの確率論で取り上げない「ベイズの定理」だ。
たとえば、よく取り上げられる例題にモンティ・ホール問題がある。
問題はこれ
「プレーヤーの前に閉まった3つのドアがあって、1つのドアの後ろには景品の新車が、2つのドアの後ろには、はずれを意味するヤギがいる。プレーヤーは新車のドアを当てると新車がもらえる。プレーヤーが1つのドアを選択した後、司会のモンティが残りのドアのうちヤギがいるドアを開けてヤギを見せる。
ここでプレーヤーは、最初に選んだドアを、残っている開けられていないドアに変更してもよいと言われる。プレーヤーはドアを変更すべきだろうか?」
正解はとにかくドアを変更する。なぜかはベイズの定理の証明となり長いので省く。
どれかのドアをあけてヤギを見せたという情報を得ることにより、行動を変えれば的中確率はあがるのだ。
言い換えると、情報を集めれば集めるほど正解に至る確率はあがる。
これは伝統的な統計論では扱ってこなかった分野ではあるが、確率の概念を大きく変えた定理である。
生活への応用は、さまざまだ。リストラされそうだ、という噂を聞いた時点では辞める、辞めないは50%だとする。どれくらいリストラされそうか、情報を獲れば得るほど、行動を変えたほうがいいのだ。
じっとしていることは愚の骨頂なのです。
おかしな話に思えるが先のサイコロ問題もベイズの定理ではしっくりする。