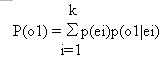条件付き確率とは一言でいうならば「得られた情報である事象を全体だ、と考え、可能性のなくなった曽事象を消滅させ、あらためて比率をとったもの」(「独習」ベイズ統計学入門より)
ということだ。(この本、すごい!)
つまり事象Bという情報を得た上での事象Aの条件付き確率は
p(B|A) = p(A & B) ÷ p(B)
(Aの事象は消えて、Bの世界だけで確率を再計算する)
つぎに式を変形すると、
p(A & B) = p(B) x p(A|B)
例えば事象Aがトランプの絵札だとし、事象Bがハートだったとする。
p(A & B) とはハートかつ絵札は3枚であることより、3/52
p(B) は13枚であることより 13/52
p(A|B)は 先の定義より、13枚であるウチの3枚なので 3/13
3/52 = 13/52 x 3/13
事象Bと情報Aを「かつ(AND)」で結んだものは、
Bの事前確率と、
Bである元でAが起きた条件付き確率の掛け算だ、
ということ。
ベイズの定理は一言でいうと「Bという情報が出たならAの事前確率を捨て、確率を1になるよう再計算したもの」